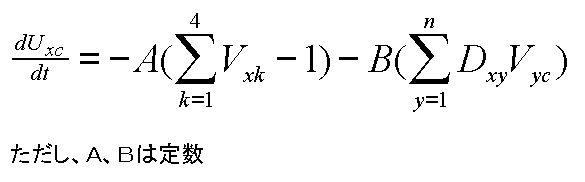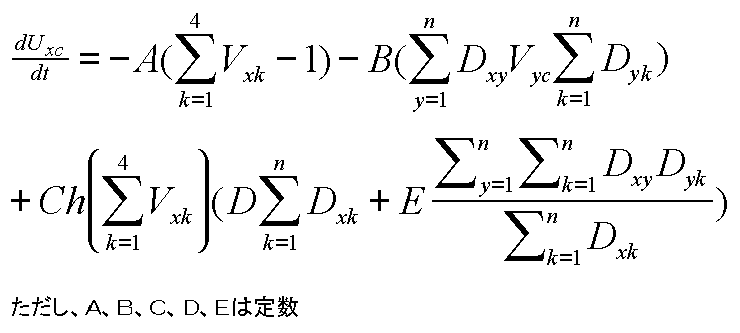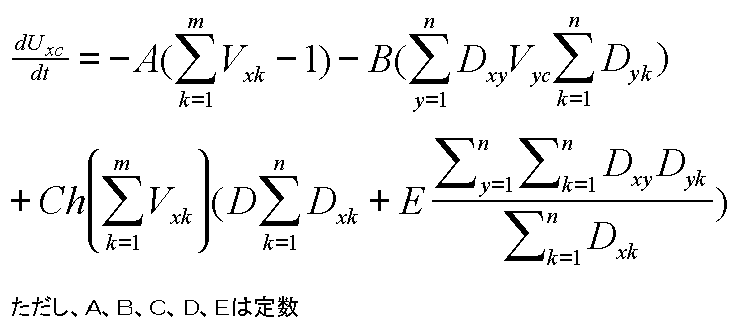係怓揾傝栤戣
栤戣
乽偁傞暯柺偺偄偔偮偐偺嬫愗傜傟偨椞堟傪係怓偺偆偪侾怓傪妱傝摉偰丄椬傝崌傢偣偺椞堟偵偼摨偠怓傪揾傜側偄傛偆偵偣傛乿偲偄偆栤戣偱偡丅嵟掅係怓偁傟偽偳傫側傕偺偱傕揾傝暘偗傞偙偲偑偱偒傞傜偟偄偱偡丅悢妛揑偵偼徹柧偼偝傟偰偄側偄偺偱偡偑丄僐儞僺儏乕僞傪巊偭偰偺徹柧偼偝傟偰偄傑偡丅悢妛揑徹柧偲僐儞僺儏乕僞傪巊偭偨徹柧偲偼壗偑堘偆偺偐撲偱偡偑丄懡偔偺悢妛幰偑僠儍儗儞僕偟丄枹偩偵徹柧偝傟偰偄側偄擄栤偱偡丅
僯儏乕儔儖昞尰
師偺傛偆側椞堟傪揾傝暘偗偰傒傞丅
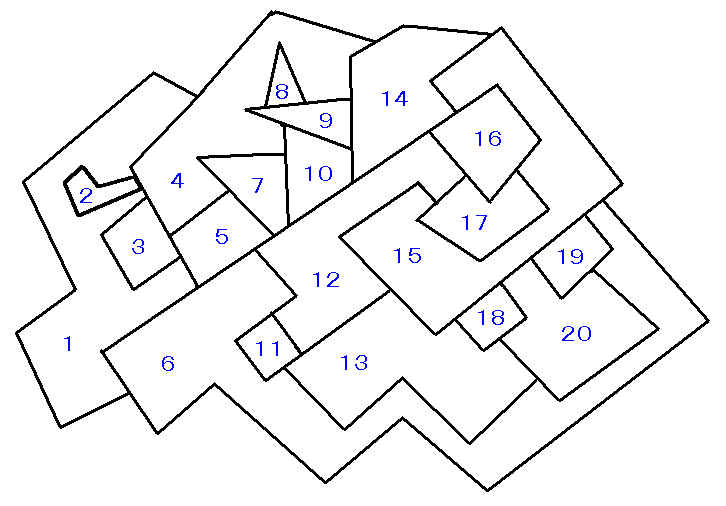
偦傟偧傟偺椞堟偵懳偟偰丄怓僯儏乕儘儞傪妱傝摉偰傑偡丅怓僯儏乕儘儞偲偄偆偺偼丄愒丄墿丄椢丄惵偺係怓偩偲偟丄崱偦傟椞堟偵椢傪妱傝摉偰偨偄偲偡傞偲丄椢僯儏乕儘儞傪敪壩偝偣偰丄偦偟偰偦偺懠偺怓僯儏乕儘儞傪捑惷壔偝偣偰偍偒傑偡丅偙傟偱丄怓偺寛掕偑偱偒傑偡丅偙偺椺偱偼丄俀侽椞堟偁傝傑偡偐傜丄係亊俀侽偺僯儏乕儘儞傪梡堄偡傟偽偄偄偙偲偵側傝傑偡丅師偵椞堟偺椬愙偟偰偄傞偐偟偰偄側偄偐傪昞偡偨傔偺攝楍俢傪梡堄偟傑偡丅攝楍俢偼丄乮椞堟悢乯亊乮椞堟悢乯丄偮傑傝偙偺椺偱偼丄俀侽亊俀侽偺攝楍偱偡丅宍幃偼丄椞堟倃偲椞堟倄偑椬愙偟偰偄偨偲偡傞偲
俢倶倷亖俢倷倶亖侾
椬愙偟偰偄側偐偭偨偲偟偨傜
俢倶倷亖俢倷倶亖侽
偲偟傑偡丅傑偨丄俢倶倶偲俢倷倷偼丄曋媂揑偵侽偲偟傑偡丅偙偆偡傞偲丄椞堟倃偲椞堟倄偲偑椬愙偟偰偄傞偐偟偰偄側偄偐偼俢倶倷偺抣傪挷傋傟偽傢偐傞傛偆偵側傝傑偡丅
摦嶌幃
倀倶們偮傑傝椞堟倃偺怓俠偺僯儏乕儘儞偺摦嶌幃傪忦審捠傝偵偨偰傞偲丄
乮愒亖侾丄墿亖俀丄椢亖俁丄惵亖係偲偟偰偄傑偡乯
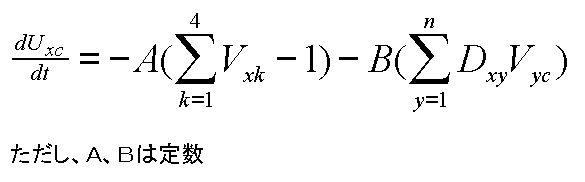
偲側傝傑偡丅
戞侾崁偼丄怓僯儏乕儘儞傪偨偩堦偮敪壩偡傞傛偆偵偟傑偡丅怓僯儏乕儘儞偑堦偮傕敪壩偟偰偄側偗傟偽丄惓偺抣傪庢傝敪壩傪懀偟丄堦偮敪壩偟偰偄傞偲侽傪庢傝忦審偺捠傝偵丄擇偮埲忋敪壩偟偰偄傞偲晧偺抣傪庢傝捔壩偺曽岦傊岦偐傢偣傑偡丅
戞俀崁偼丄乽椬愙椞堟傪摨偠怓偱揾傜側偄乿偲偄偆忦審傪昞偟偰偄傞丅怓俠偵偮偄偰椞堟倃偵椬愙偟偐偮敪壩偟偰偄傞椞堟偺崌寁屄悢偱偡丅偮傑傝丄偙偺悢偑侽側傜偽丄忦審捠傝偱偁傝丄堦偮偱傕偙傟偵奩摉偡傞椞堟偑偁偭偨偲偡傟偽丄偦偺僯儏乕儘儞傪捔壩偺曽岦傊岦偐傢偣傑偡丅忋偱俢倶倶偮傑傝倷亖倶偺偲偒俢倶倶亖侽偲偟偰傑偟偨偑丄偙偙偱曋棙偑偄偄傛偆偵偡傞偨傔偱偡丅帺暘帺恎傪悢偊傞昁梫偑側偄偺偱俢倶倶亖侽偲偟偰偍偗偽丄帺暘帺恎偑敪壩偟偰偄傛偆偑偟偰傑偄偑僇僂儞僩偝傟側偔側傝傑偡丅
摦嶌幃偼丄偙傟偱姰帏偲巚偄偒傗晄姰慡側傫偱偡丅偦傟偼側偤偐偲偄偆偲丄椬偺椞堟偑偡傋偰偺怓傪巊偄愗偭偰偟傑偭偨傜丄偨偪傑偪摦嶌幃偼丄巚偄捠傝偵摦偐側偔側傝傑偡丅嬶懱揑偵偄偆偲丄師偺傛偆側壴乮丠乯傪峫偊偰傒傞丅
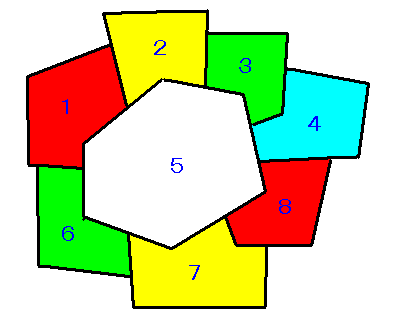
恀傫拞偺椞堟俆偼丄廃傝偺椞堟偑偡傋偰偺怓傪巊偭偰偄傞偺偱偳偺怓傕揾傞偙偲偑偱偒傑偣傫丅摦嶌幃偺抣偼丄戞堦崁偼怓僯儏乕儘儞傪敪壩偵摫偄偰偄偒傑偡偑丄戞俀崁偼丄捔惷傪懀偟偰偄偒傑偡偐傜寢嬊偺偲偙傠椞堟俆偼丄偳偺怓僯儏乕儘儞傕敪壩偟側偄偙偲偵側傝傑偡丅偙偆偄偆忬懺偵娮傜側偄傛偆偵惓婯壔傪峴偄傑偡丅椬傝崌偆椞堟偑懡偄椞堟偐傜丄偮傑傝懠偺椞堟傊偺塭嬁椡偺戝偒側椞堟偐傜怓傪寛掕偡傞傛偆偵偟傑偡丅惓婯壔偝傟偨摦嶌幃偼丄
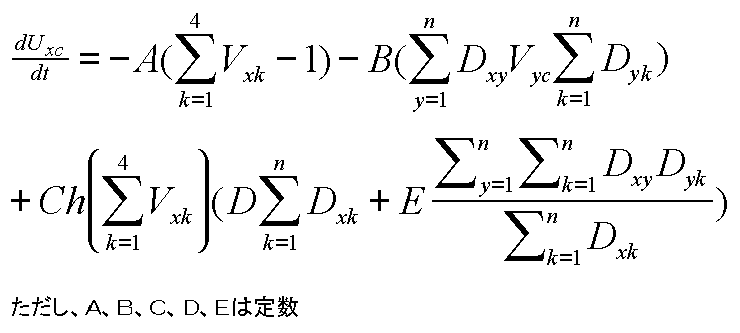
偲側傝傑偡丅掕悢俢偲椞堟偺椬愙忦審偺俢傪庢傝堘傢側偄傛偆偵丅
戞侾崁偼丄尒偰偺捠傝慜偲摨偠偱偡丅
戞俀崁偼丄嚁俢倷倠傪妡偗傞偙偲偵傛偭偰丄懡偔偺椬傝崌偆椞堟傪帩偭偨椞堟偱偁傟偽偁傞傎偳丄傛傝偦偺椞堟偐傜偺梷惂傪庴偗傞傛偆偵側傝傑偡丅
戞俁崁偼丄僸儖僋儔僀儈儞僌僞乕儉崁偱偡丅僸儖僋儔僀儈儞僌偼丄怓僯儏乕儘儞偑堦偮傕敪壩偟偰偄側偗傟偽丄敪壩傪懀偟傑偡丅屻傠偵妡偗偰偁傞偺偼丄俢嚁俢倶倠偼丄椞堟倃偺椬傝崌偆屄悢丄俤嚁嚁俢倶倷俢倷倠乛嚁俢倶倠偼丄椞堟倃偺椬愙椞堟偺椬愙椞堟偺暯嬒屄悢偱偡丅偙傟傜偺榓傪僸儖僋儔僀儈儞僌僞乕儉崁偵妡偗傞偙偲偵傛偭偰椬愙椞堟偺懡偄椞堟偮傑傝塭嬁椡偺戝偒側椞堟偐傜怓傪寛掕偟偰偄偔偙偲偑偱偒傑偡丅俢嚁俢倶倠偼丄巕偺悢丄俤嚁嚁俢倶倷俢倷倠乛嚁俢倶倠偼丄懛偺悢偲偄偭偨傛偆側僀儊乕僕傪帩偭偰傕傜偊傟偽傢偐傝傗偡偄偺偱偼側偄偐偲巚偄傑偡丅
戝曄尒偨栚偼傢偐傝偵偔偦偆偵尒偊傑偡偑偠偭偔傝幃傪偍偭偰偄偭偰偔偩偝偄丅
僾儘僌儔儈儞僌
崱夞偼丄夝偑偆傑偔弌傞傛偆偵偡傞偺偵嬯楯偟傑偟偨丅摦嶌幃捠傝傗偭偰傕夝偑側偐側偐弌傑偣傫偱偟偨丅俙俛俠俢俤偺掕悢抣偺挷惍傗儊僀儞僾儘僙僗側偳傪岺晇偟傑偟偨丅嬶懱揑偵偼俙亖俁侽丄俛亖俠亖俢亖俤亖侾偵丄傑偨丄儊僀儞僾儘僙僗偺曽偱偼丄怓僯儏乕儘儞偺摦嶌偺弴斣傪儔儞僟儉偵峴偆側偳偟傑偟偨丅
椬愙忦審偼丄暿僼傽僀儖偐傜撉傒崬傒傑偡丅彂幃偼丄
20
0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,1,1,0,1,0,1,1,1,1,0,0,0,1,0,0,0,0,0,0
1,0,1,1,0,1,1,0,0,0,0,1,0,0,0,0,0,0,0,0
1,0,0,0,1,0,0,0,0,0,1,1,1,0,1,0,0,0,1,1
0,0,0,1,1,0,0,0,0,1,0,1,0,0,0,0,0,0,0,0
0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0
0,0,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,0
0,0,0,1,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0
0,0,0,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,0,0
0,0,0,0,1,1,1,0,0,1,1,0,1,1,1,1,1,0,0,0
0,0,0,0,0,1,0,0,0,0,1,1,0,0,1,0,0,1,0,1
0,0,0,1,0,0,0,0,1,1,0,1,0,0,1,1,0,0,0,0
0,0,0,0,0,1,0,0,0,0,0,1,1,1,0,1,1,1,1,1
0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,1,0,0,0
0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,1,0,0,0,0
0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0,1
0,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,1
0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,1,1,0
偺傛偆偵偼偠傔偵椞堟悢丄偦偺偁偲偵椬愙忦審傪乭,乭偱嬫愗偭偰擖傟偰偔偩偝偄丅
椬愙忦審偼丄幬傔偵懳徧側偺偱曅懁偩偗偺擖椡偵偟偰傕偄偄偺偱偡偑丄娫堘偄傪傛傝杊偖偨傔偵慡晹擖椡偡傞宍傪庢傝傑偟偨丅懳徧偱側偄僨乕僞偑搉偝傟傞偲偼偠偔傛偆偵側偭偰傑偡丅
4Color.lzh (15KB)
丂丂4Color.c 丂丂丂丂僜乕僗僼傽僀儖
丂丂4Color.exe 丂丂幚峴宍幃僼傽僀儖
丂丂4C_00.dat丂丂丂椺偺椬愙忦審僨乕僞
椺偺栤戣偺夝偼丄
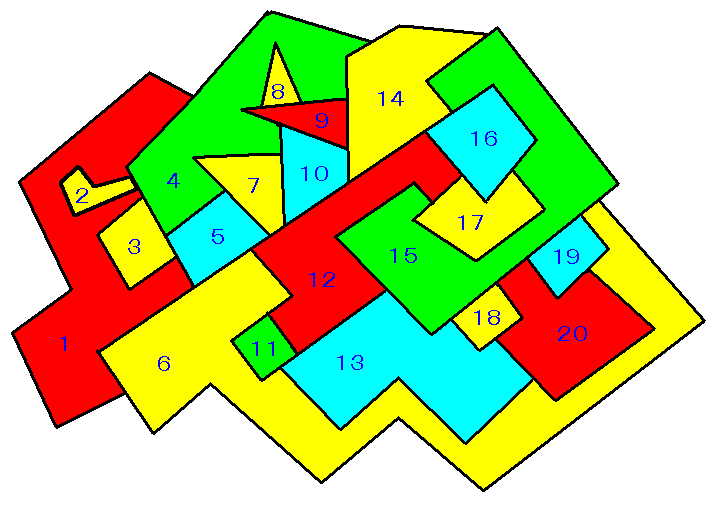
傑偨丄係怓偱側偔偰倣怓偱揾傝暘偗偨偄偲偡傟偽丄摦嶌幃傪師偺傛偆偵曄峏偡傞偩偗偱偄偗傑偡丅
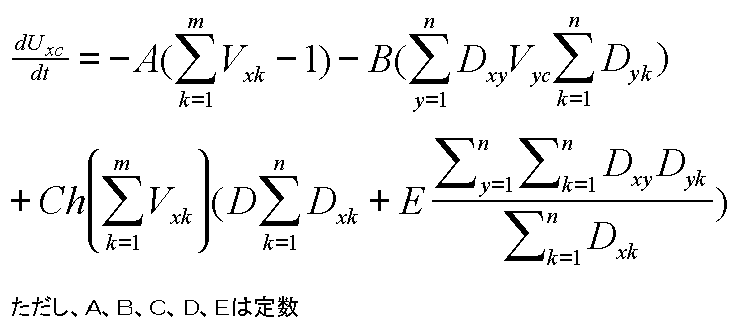
崱夞偼丄寢峔崪偑愜傟傑偟偨丅杮偑寢峔偆偦偭傁偪傪楢敪偟偰偄偨偺偱丅
栠傞丂僀儞僨僢僋僗傊丂師傊