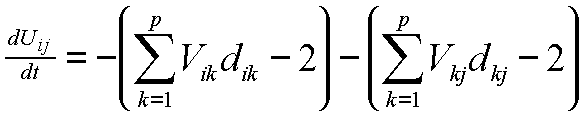
今回、無意味っぽい定数なしです。
第一項は、i行目のニューロンを2つ発火させるようにはたらきます。
第二項は、同じくj列目のニューロンを2つ発火させるようにはたらきます。
ただ単純に縦横にニューロンを発火させるのではなくdをかけることによってナイトの可能な動きのみにニューロンを発火させることができます。なぜ、2つ発火させるのかと思うと思います。それは、ひとつのマス目をただ一回だけ通るときそのマスに一回だけ入ってきて一回だけ出て行きます。i→j→k番目と動くとすると
ナイト巡回問題
問題
ナイトをチェス盤のあるマス目から出発してすべてのマス目を1回ずつ通りもとに戻ってくるような道を見つめる問題です。チェス盤のように8×8のマス目だけではなく一般化してm×nのマス目で考えることにします。
ニューラル表現
まず、p×pの2次元ニューロン配列を用意します。pはマス目の数です。m×nの盤なら
p=mn
です。ニューロンVijが発火していれば、i→j(もしくは、j→i)への動きを表します。ただし、i、jはマス目にふった番号。例えば、4×4の場合
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
にふる。また、ナイトが可能な動きを表すp×pの2次元配列dを用意します。d(1,7)=1だったとしたらマス1から7へ移動可能だということを示します。d(2,1)=0なら2から1へは移動できないというように可能なら1、不可能なら0とします。また、i→jという動きが可能ならj→iという動きも可能なはずです。ということは、常に
dij=dji Vij=Vji ・・・・・・・・ (1)
が成り立つということになります。
動作式
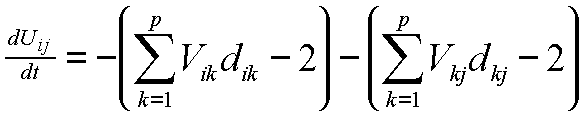
今回、無意味っぽい定数なしです。
第一項は、i行目のニューロンを2つ発火させるようにはたらきます。
第二項は、同じくj列目のニューロンを2つ発火させるようにはたらきます。
ただ単純に縦横にニューロンを発火させるのではなくdをかけることによってナイトの可能な動きのみにニューロンを発火させることができます。なぜ、2つ発火させるのかと思うと思います。それは、ひとつのマス目をただ一回だけ通るときそのマスに一回だけ入ってきて一回だけ出て行きます。i→j→k番目と動くとすると
Vij=Vkj=1
です。ナイトが巡回するように動かすのだからどっち回りでも動いてもよいのであまりどこからどこへという方向にはとらわれずにただ入ってきて出ていくのに縦横2つずつ発火させると考えるととっつきやすいのではないかと思います。
ほんまにこんなんでうまくいくのかと思われる方がいると思います。そうです。うまくいかないのです。この動作式は,マス目を一度だけ通り、通り道が閉じているつまりわっか(ぐるぐる回れる)になっているれば満たします。何がいいたいかというとすべてのマスがつながっているということが抜けているのです。4×3の盤の例で示すと
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
ニューロン配列:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | ■ | ■ | ||||||||||
| 2 | ■ | ■ | ||||||||||
| 3 | ■ | ■ | ||||||||||
| 4 | ■ | ■ | ||||||||||
| 5 | ■ | ■ | ||||||||||
| 6 | ■ | ■ | ||||||||||
| 7 | ■ | ■ | ||||||||||
| 8 | ■ | ■ | ||||||||||
| 9 | ■ | ■ | ||||||||||
| 10 | ■ | ■ | ||||||||||
| 11 | ■ | ■ | ||||||||||
| 12 | ■ | ■ |
でもうこれ以上ニューロンは動かなくなります。これを実際の道におこしてみると
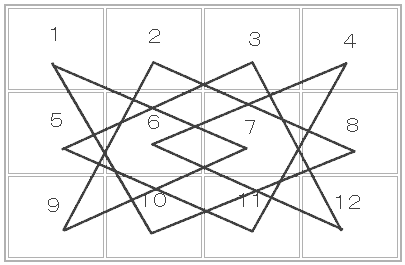
となり、ひとつの道ですべてのマスを通っておらず2つの道でマスを回っています。
プログラミング
今回は、たくさんの配列を用意しなければならないのでLSI C−86試食版のスモールモデルでは、二桁×二桁のとき領域が確保できません。だから、ほかのコンパイラでコンパイルしたものを付けときます。32bit下(DOS窓)でしか動きません。
今までは、再コンパイルしないと変数が変えられなかったが、今回は外部にコンフィグファイルを用意してみました。
knight.cfg:
NROW = 8
NCOLUMN = 8
A = 1
UTP = 3
LTP = 1
UMAX = 10
UMIN = -10
CHECKER = 1
CHECK_MAX = 600
順番を変えたり一行に二つ以上書いたりすると正常に動かなくなるので注意してください。
ナイトの移動判定dは、自動生成します。その他、目新しいことは何にもやっていないので説明することないです。
上のほうにある(1)をうまく利用すると確保する領域をRとすると
R=p(p−1)/2
で済みます。めんどっちいのでやってません。
Knight.c ソースファイル
Knight.exe LSI C−86試食版でコンパイルしたもの
Knight32.exe 32bit下での実行ファイル
knight.cfg コンフィグファイル、knight.exeとknight32.exe共通
ますの数が大きくなってくると解が出にくくなります。根気強く実行してください。
あと、1943年にFred Schuh氏が述べたことでm×nのm、nはともに偶数でなければならないらしいです。解があるための必要条件です。また、正方形の場合は、6以上で偶数であれば解が一つは存在するようです。