ニューラルネットワークとは
ニューラルネットワークとは、1982年ホップフィールドらが提唱した物で、
脳の仕組みの一部を数学的にモデル化した物です。
神経細胞網をコンピューター上でシュミレーションするような物です。
まず、神経細胞網を構成する単位から見ていきましょう。
神経細胞「ニューロン」は、「発火している(興奮している)」または、「発火していない(興奮していない)」という
どちらかの状態を取ります。ニューロンモデルは、ニューロンの状態を指すパラメータとニューロンの発火状態
との関係です。あるニューロンの状態を示すパラメータをUと表し、発火状態をVで表します。
Vは、発火していると1、発火していないと0を取るようにします。モデルとして、たとえば、
Uが5より大きい時Vは、1、それ以下だと0をといったもの。
if ( U > 5 ) V = 1;
else V = 0;
マッカロック・ピッツニューロン


ニューロンモデルの中でもっとも単純なモデルは、マッカロック・ピッツモデルと呼ばれるものです。
このニューロンモデルは、1943年にマッカロックとピッツという学者によって提唱され、
ニューラルネットワークの研究の先駆けとなったものです。
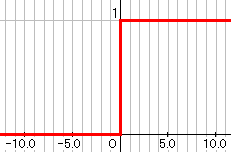
Uの値の高低によってのみでVを決定します。上左図は、境目の値(閾値)0によって
Vの値を決定しているときのグラフです。このようなニューロンのことをマッカロック・ピッツニューロンと
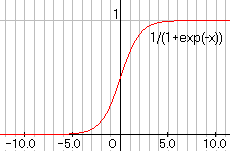
いいます。このモデルは、上右図のシグモンド関数を単純化して作られたものです。
if ( U > BORDER ) V = 1;
else V = 0;
ヒステリシス−マッカロック・ピッツニューロン
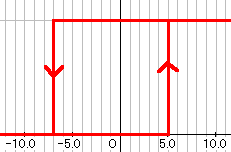
このモデルは、マッカロック・ピッツモデルに二つの閾値を設けたものです。
閾値UTP(Upper Trip Point)を越えると発火して、閾値LTP(Lower
trip Point)より小さくなれば、
発火が消えます。上図は、UTP=5、LTP=−7のときの図です。
if ( U > UTP ) V = 1;
if ( U < LTP ) V = 0;
このモデルは、一度発火したニューロンは消えにくく、また逆に一度消えてしまったニューロンは、
発火しにくいといった性質を持っています。
マキシマムニューロン
マキシマムニューロンとは、ある数のニューロンをひとかたまりとして、それらのUの値を比較し、
最大の値のニューロンのみ発火させるというもの。このモデルの目的は、一つだけニューロンを発火させる
というもので、もし、最大が複数個あるならば、どれか一つ発火させることになると思います。
また、閾値を設定して、最大値が閾値を越えていなかったらまったく発火させないでいるのもいいでしょう。
MAX = 1;
UMAX = U[1];
for ( i = 2; i <= n; i++ ) {
if ( U[i] > UMAX ) {
UMAX = U[i];
MAX = i;
}
}
if ( U[MAX] > BORDER ) V[MAX] = 1;
ニューラルネットワークの仕組み
いままでの話は、個々のニューロンについての話でした。今度は、それらをひとまとまりのネットワークとして
働かす為にどのように個々のニューロンを相互作用させていくかです。
ニューラルネットワークは、個々のニューロンを「動作式」という数学的にモデル化された式によって
制御します。それぞれのニューロンが動作式を持っています。動作式によって結びつけられたニューロンは、
それらの発火状態Vを考慮し、自分の状態Uを変化させていきます。つまり、ニューラルネットワークとは、
「動作式によって個々のニューロンの状態Uを変化させ、発火状態Vを決定していく」という一連の作業を
繰り返すことによって解を導いていくというものです。
ここまでの話では、なんこっちゃようわからんと思います。それは、「動作式」というものの説明していないからだ
と思います。動作式の説明は、次の具体的な例(Nクイーン問題)を用いて説明していきたいと思います。