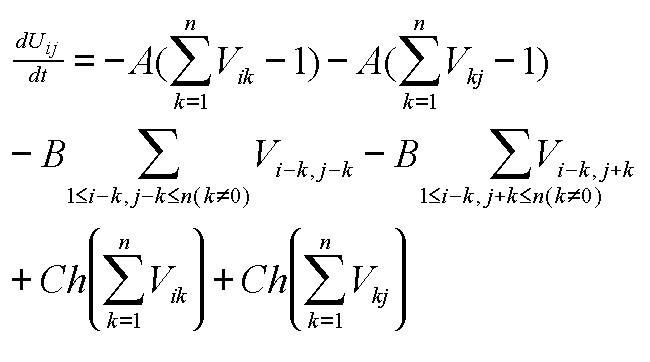Nクイーン問題をニューラる
NNの部屋を作った当初の自分の考えていたニューラルネットワーク像と今の自分の像がかなり違っています。一通り以前思っていたとおりにやってから厳密なNNの話に移りたいと思います。当初というのは、組み合わせ最適化問題に特化したものです。
それでは、Nクイーン問題をニューラってみましょう。
Nクイーン問題とは
もうご存じだと思いますが、念のため
「n×nのマス上に、n個のクイーンをどのクイーンも互いに効き当たらないように並べよ」というものです。
ニューラル表現する
まず、n×nのマスに対応する2次元配列Vを用意する。そうすれば、(i、j)にクイーンが置いてあるかどうかは、
Vij = 0 or 1 で表すことができる。また、それぞれのニューロンの状態を確保するn×nの2次元配列Uを用意する。これでニューラル表現は、完了。
動作式を作る
マッカロック・ピッツニューロンを用いた(i,j)のニューロンの動作式は、次のようなものです。
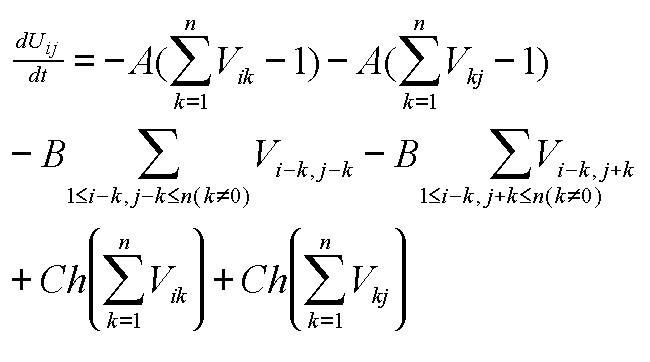
A,B,Cは、定数。(ここではA,B、C=1にしてます)
第一項は、i行に一つニューロンが発火するように(クイーンを一つ置くように)制約してしています。条件を満たしている(一行に一つ発火してる)と値は0となります。たくさん発火していた場合はより絶対値の大きな負の値を取りニューロンを沈静の方向に向かわせます。
第二項は、第一項のようにしてj列のニューロンを制約します。
第三項は、ようく式を追って見たらわかると思いますが、(i,j)を含めない右下がりの斜めのニューロンが効きあっていないかを制約しています。
第四項は、右上がりの斜めのニューロンを制約してます。
第三、四項で、斜めに関して(i,j)も含めて0個か1個のニューロンが発火するようにしてます。それは、(i,j)を含まずたとえ斜めに一つも発火していなかったとしても、そこの発火を促せばよいとは限らなし、(i,j)が発火していたら、斜めが発火していないことが条件ですし。
第五、六項についてはまず、関数h(x)を次のように定義します。
x = 0の時 h(x) = 1;
x≠0の時 h(x) = 0;
C言語で書くと
int h( int x )
{
if ( x = 0 ) return 1;
else return 0;
}
つまり、縦横に一つもニューロンが発火していなかったら、発火を促すというものです。これは、ヒルクライミングタームと呼ばれるものでニューラルネットワークの状態が極小解に陥ったときそれを脱出する働きがあるものです。
自分の持っている本には、極小解の例として6×6の問題で
0 0 0 1 0 0
0 0 0 0 0 1
1 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 1 0
0 0 1 0 0 0
というものをあげています。しかし、C=0としてdU/dtを計算してみると
-1 +1 -1 0 -1 0
0 -1 -1 0 -1 0
0 0 -1 0 -1 -2
-1 +1 +1 -1 0 0
0 0 -2 -1 0 0
0 0 0 -2 0 -1
となります。発火に向かうニューロンがあるの極小解になっていないような気がするんです。
第一、二項は、i行j列に発火してるニューロンがなかったら値は正(=2)を取るので斜めに二つのニューロンがなければ、発火を促していることになります。自分が思うにヒルクライミングターム的な働きを第一、二項がすでに持っているような気がします。自分の持っている本は、結構間違いが多い(ソースに)のでもしかしたら極小解の例が間違ったものなのかもしれません。まあ、とにかく第五、六項については、極小解を抜け出るためのヒルクライミングタームと呼ばれているものというのを覚えてもらえればいいと思います。なんならそれ以外は、読まなかったことにしてください(笑
念のためC=1の時dU/dtがどんな値を取るのか載っけておきます。
-1 +2 -1 0 -1 0
0 0 -1 0 -1 0
0 +1 -1 0 -1 -2
0 +2 +2 0 +1 +1
0 +1 -2 -1 0 0
0 +1 0 -2 0 -1
動作式を使う
どのように動作式を使うのでしょうか?それを見ていきましょう。
それには、1次オイラー法というものを利用します。
U(t+1)=U(t)+dU(t)
この式が表しているのは、時間tにおけるUの値をU(t)とすると次の時間t+1のUの値は、dU/dtつまり動作式の値を足した値という意味です。これをすべてのニューロンについて繰り返し行っていきます。もちろん、Uの値の変化に伴ってVも変化させていき、発火しているニューロンのdUがすべて0であり、正の値のdUが一つもないとき解となるのです。
それでは、Uの変化についてVをどのように変化させていけばよいのでしょうか?
大きく分けて2通りのやり方があります。まず、
@連続モデル(sequential model)
for ( i = 1; i <= n; i++ ) {
for ( j = 1; j <= n; j++ ) {
U[i][j] += dU[i][j];
if ( U[i][j] > 0 ) V[i][j] = 1;
else V[i][j] = 0;
}
}
見てもらえればわかると思いますが、各ニューロンのUの値を変化させてすぐにVの値も変化させています。
@並列同期モデル(synchronous parallel model)
for ( i = 1; i <= n; i++ ) {
for ( j = 1; j <= n; j++ ) {
U[i][j] += dU[i][j];
}
}
for ( i = 1; i <= n; i++ ) {
for ( j = 1; j <= n; j++ ) {
if ( U[i][j] > 0 ) V[i][j] = 1;
else V[i][j] = 0;
}
}
こちらは、すべてのニューロンのUの値を変化させた後に、Vの値を変化させています。
もう一つ並列同期モデルを派生させて作った並列非同期モデルというものもあります。
for ( i = 1; i <= n; i++ ) {
for ( j = 1; j <= n; j++ ) {
U[i][j] += dU[i][j];
}
}
for ( i = 1; i <= n; i++ ) {
for ( j = 1; j <= n; j++ ) {
if ( random > x ) {
if ( U[i][j] > 0 ) V[i][j] = 1;
else V[i][j] = 0;
}
}
}
Vの値を適宜ランダムで変えてやろうというものです。
これで一通りNクイーン問題について話ができていると思います。もしかしたら、説明が悪いすぎるのでわかりにくすぎたりしているところがあるかもしれません。そんなときは、メールや掲示板でどんどん質問してほしいです。皆さんにいろいろ質問されたり、指摘させたりしてよりよいものができてくると思います。じゃんじゃん質問、ご指摘待ってます。
次回には、ソースコードを掲載したいと思います。いまもあるんですけど、汚いし、注釈もぜんぜんはいっていないので非常に見にくい(醜い?)状態にありますので、改善でき次第公開したいと思っています。それと、本には、マッカロック・ピッツニューロンを用いたものしかNクイーン問題に関しては、載っていませんが、たぶんいけるであろうマキシマムニューロンを説明がてら用いてやってみようと思います。
前へ インデックスへ 次へ